Fantasy Premier League Classification Model Using Scikit Learn
A Supervised Learning Classification Model Example Using Scikit Learn
This is my attempt at producing a classification model in Python using the Scikit-Learn package. I’m going to use Fantasy Premier League player data from the 2017/18 season to create a model that will attempt to predict the position of a player given their player stats. There are four possible prediction classes: Goalkeeper, Defender, Midfielder, Forward.
Notes on the Data
The CSV file containing the player data has been preprocessed into a format compatible with Scikit-Learn. All the stats (feature) columns were numerical anyway so there were no categorical variables that needed dealing with. There is no missing data in any of the columns of the dataset.
Players could be on the field accruing stats for up to 3420 minutes (38 full matches) during the season, indeed 10 players did just that. I removed all players from the dataset who played less than 180 minutes (the equivalent of 2 full matches). That still leaves lots of players who will have played far less than others and their comparative lack of stats will no doubt impact on model performance. As this is an example rather than a model intending to have any great practical use I’ll proceed while understanding that limitation is there.
The target column ‘Position’ will need to be processed as it contains strings (GK, DF, MF, FW). As I understand it in scikit-learn the prediction classes need to be numerical values, I’ll show how to encode that column using scikit-learn LabelEncoder.
Importing our Dataset
#Import relevant packages
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import itertools
#Import our CSV data file as a dataframe
fpl_data = pd.read_csv('https://eddiesport.github.io/projects/FPL_final.csv', \
header=0, index_col=0, encoding='cp1252')
print(fpl_data.head())
print(fpl_data.info())
Position Goals Scored Assists Clean Sheets \
Full Name
Eldin Jakupovic GK 0 0 0
Jeremy Pied DF 0 1 0
Kyle Walker Peters DF 0 2 1
Beni Baningime MF 0 0 0
Konstantinos Mavropanos DF 0 0 1
Goals Conceded Own Goals Penalties Saved \
Full Name
Eldin Jakupovic 6 0 0
Jeremy Pied 3 0 0
Kyle Walker Peters 4 0 0
Beni Baningime 2 0 0
Konstantinos Mavropanos 5 0 0
Penalties Missed Yellow Cards Red Cards Saves \
Full Name
Eldin Jakupovic 0 0 0 8
Jeremy Pied 0 0 0 0
Kyle Walker Peters 0 0 0 0
Beni Baningime 0 1 0 0
Konstantinos Mavropanos 0 0 1 0
Bonus Points Bonus Point System Score Influence \
Full Name
Eldin Jakupovic 0 36 67.8
Jeremy Pied 1 47 65.8
Kyle Walker Peters 0 73 70.4
Beni Baningime 0 20 9.4
Konstantinos Mavropanos 0 41 52.2
Creativity Threat ICT Index
Full Name
Eldin Jakupovic 0.0 0 6.8
Jeremy Pied 29.9 4 10.0
Kyle Walker Peters 48.3 10 12.9
Beni Baningime 3.8 0 1.3
Konstantinos Mavropanos 1.3 2 5.5
<class 'pandas.core.frame.DataFrame'>
Index: 441 entries, Eldin Jakupovic to Asmir Begovic
Data columns (total 17 columns):
Position 441 non-null object
Goals Scored 441 non-null int64
Assists 441 non-null int64
Clean Sheets 441 non-null int64
Goals Conceded 441 non-null int64
Own Goals 441 non-null int64
Penalties Saved 441 non-null int64
Penalties Missed 441 non-null int64
Yellow Cards 441 non-null int64
Red Cards 441 non-null int64
Saves 441 non-null int64
Bonus Points 441 non-null int64
Bonus Point System Score 441 non-null int64
Influence 441 non-null float64
Creativity 441 non-null float64
Threat 441 non-null int64
ICT Index 441 non-null float64
dtypes: float64(3), int64(13), object(1)
memory usage: 62.0+ KB
None
We can see that the created DataFrame contains the players names as the index and 17 data columns. None of the columns appears to have missing data (as expected given its been preprocessed). The 16 numerical columns are going to be our features while the ‘Position’ column will be our target. Lets encode this column now so scikit-learn will accept it.
Encoding our Feature Column
#Using Label Encoder
from sklearn.preprocessing import LabelEncoder
#Instantiate an example of LabelEncoder
le = LabelEncoder()
#Apply to our target column
fpl_data.Position = le.fit_transform(fpl_data.Position)
#Create a dictionary to show our newly encoded key/value pairs
#The class_names variable will also be used in our visualizations later
class_names = le.classes_
values = le.transform(le.classes_)
dictionary = dict(zip(class_names, values))
print(dictionary)
{'DF': 0, 'FW': 1, 'GK': 2, 'MF': 3}
As we can see, our target classes are now numeric, with 0 representing ‘DF’, 1 for ‘FW’, etc.
Create our Feature and Target Arrays
#Create feature (X) and target (y) arrays
feature_cols = ['Goals Scored', 'Assists', 'Clean Sheets', 'Goals Conceded', 'Own Goals', 'Penalties Saved', \
'Penalties Missed', 'Yellow Cards', 'Red Cards', 'Saves', 'Bonus Points', 'Bonus Point System Score', \
'Influence', 'Creativity', 'Threat', 'ICT Index']
X = fpl_data.loc[:, feature_cols]
print(X.shape)
y = fpl_data.Position
print(y.shape)
print(y.value_counts())
(441, 16)
(441,)
3 182
0 159
1 66
2 34
Name: Position, dtype: int64
Something to note is the class imbalance of our target variable, for example we have far more midfielders (182) than goalkeepers (34). This is something to bear in mind when looking at the results of testing our model later.
A Visualization of our Feature Columns
I should have done some graphical EDA earlier to see if relationships between our feature columns existed. As I’ve just separated the feature columns out I’ll produce a correlation matrix of all our 16 variables. Given there are quite a lot of variables I’ll then create a heatmap of the result.
#Create a show a correlation matrix of the feature columns
corr_mat = X.corr()
#Visualize this matrix using Seaborns heatmap function
sns.heatmap(corr_mat)
plt.title('Feature Columns Correlation Heatmap')
plt.show()
plt.clf()

Unsurprisingly there are a range of relationships here, ‘Goals Scored’ and ‘Threat’ are highly correlated, while ‘Penalities Saved’ and ‘Creativity’ are not. There’s certainly enough going on that one should hope a useful classification model could be trained using the data, so lets continue!
Scaling our Data
If the various columns of data cover differing ranges (from min to max values in each column) then we should look into rescaling our data. Lets take a look.
#Quick look at the DataFrames column data statistical details
print(fpl_data.describe())
Position Goals Scored Assists Clean Sheets Goals Conceded \
count 441.000000 441.000000 441.000000 441.000000 441.000000
mean 1.541950 2.235828 2.047619 5.773243 25.090703
std 1.341195 3.784980 2.813926 4.104688 14.925601
min 0.000000 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 3.000000 13.000000
50% 1.000000 1.000000 1.000000 5.000000 24.000000
75% 3.000000 3.000000 3.000000 9.000000 34.000000
max 3.000000 32.000000 18.000000 19.000000 63.000000
Own Goals Penalties Saved Penalties Missed Yellow Cards \
count 441.000000 441.000000 441.000000 441.000000
mean 0.068027 0.047619 0.054422 2.612245
std 0.301357 0.277980 0.280802 2.329989
min 0.000000 0.000000 0.000000 0.000000
25% 0.000000 0.000000 0.000000 1.000000
50% 0.000000 0.000000 0.000000 2.000000
75% 0.000000 0.000000 0.000000 4.000000
max 4.000000 3.000000 3.000000 11.000000
Red Cards Saves Bonus Points Bonus Point System Score \
count 441.000000 441.000000 441.000000 441.000000
mean 0.088435 4.863946 5.467120 323.800454
std 0.299814 20.584738 5.960814 201.358017
min 0.000000 0.000000 0.000000 11.000000
25% 0.000000 0.000000 0.000000 167.000000
50% 0.000000 0.000000 4.000000 305.000000
75% 0.000000 0.000000 9.000000 470.000000
max 2.000000 145.000000 31.000000 913.000000
Influence Creativity Threat ICT Index
count 441.000000 441.000000 441.000000 441.000000
mean 390.402268 252.426531 268.795918 91.133560
std 261.424449 268.366338 321.296859 71.471795
min 8.800000 0.000000 0.000000 1.300000
25% 181.800000 59.400000 55.000000 36.800000
50% 353.800000 164.700000 150.000000 76.900000
75% 550.400000 340.700000 361.000000 120.600000
max 1496.200000 1744.200000 2355.000000 454.400000
We can see a large variation in ranges, eg, ‘Penalties Saved’ ranges from 0-3, while Threat ranges from 0-2355. This suggests we should include scale our data within the model. I’ll do this using Standardization.
What Type of Classification Model To Use?
Scikit-learn gives lots of choices, I’m going to use a K-Nearest Neighbors (k-NN) classifier here. To be more thorough one could try many models and see which performs better given your metrics of choice.
Create a Pipeline Object
I’m going to standardize my data, then apply the k-NN model. This is two seperate steps, so I’ll put them in a pipeline!
#Import required scikit-learn modules
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
#Set up the pipeline steps
steps = [('scaler', StandardScaler()),
('knn', KNeighborsClassifier())]
#Create the pipeline object
pipeline = Pipeline(steps)
Hyperparameter Tuning
We are going to tune the n_neighbors parameter of our k-NN classifier. To do this I’ll create a range of ‘n_neighbors’ to try. I’ll use 1-20 here.
#Define parameter grid for K neighbors search
k_range = np.arange(1, 21)
parameters = {'knn__n_neighbors': k_range}
Train Test Split
Lets create our training and test sets. Add in a random state for repeatability of results.
#Create training and test (hold out) sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state=42, stratify=y)
Instantiate a GridSearch Object
Lets add our pipeline and parameters to a gridsearch object. Cross validation is set to 3 subsets by default, I’ll change it to 5 here. The result of this will be, for bettor or worse, our model.
#Instantiate GridSearch object.
fpl_model = GridSearchCV(pipeline, parameters, cv=5)
Train and Test our Model, show Model Metrics
#Fit model to training set
fpl_model.fit(X_train, y_train)
#Predict labels of the test data
y_pred = fpl_model.predict(X_test)
#Compute and print metrics
from sklearn.metrics import classification_report, confusion_matrix
#Print accuracy, classification report and the best model parameters used
print('Accuracy: {}'.format(fpl_model.score(X_test, y_test)))
print(classification_report(y_test, y_pred))
print("Tuned Model Parameters: {}".format(fpl_model.best_params_))
Accuracy: 0.7297297297297297
precision recall f1-score support
0 0.69 0.78 0.73 40
1 0.79 0.65 0.71 17
2 1.00 0.88 0.93 8
3 0.71 0.70 0.70 46
avg / total 0.74 0.73 0.73 111
Tuned Model Parameters: {'knn__n_neighbors': 3}
An accuracy score of 0.7298. Well its a lot better than guessing that everyone was a Midfielder (the most numerous class), that would have yielded an accuracy score of 0.41, so our model is definitely working. From our hyperparameter tuning we can see the optimum number of ‘n_neighbors’ in this case was 3.
Lets look at another model metric, the confusion matrix. The following code that defines a function for visualizing a confusion matrix is not mine, its taken from the scikit-learn docs. The first example is not normalized, the second one is. Normalizing is a good idea here because of the class imbalance we mentioned earlier.
#Function to visualize the confusion matrix
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, y_pred)
#Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
#Plot normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
title='Normalized confusion matrix')
plt.show()
Confusion matrix, without normalization
[[31 0 0 9]
[ 2 11 0 4]
[ 1 0 7 0]
[11 3 0 32]]
Normalized confusion matrix
[[ 0.775 0. 0. 0.225 ]
[ 0.11764706 0.64705882 0. 0.23529412]
[ 0.125 0. 0.875 0. ]
[ 0.23913043 0.06521739 0. 0.69565217]]
<matplotlib.figure.Figure at 0xc08beb8>
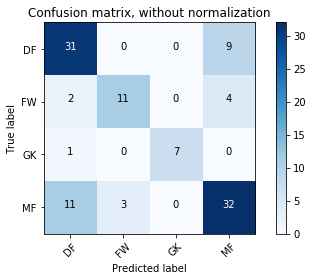
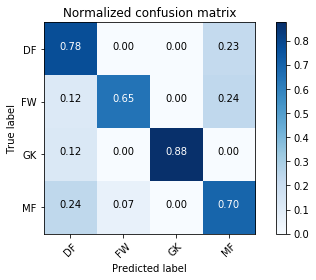
We can see from the normalized confusion matrix that the model was good at predicting goalkeepers on the test set, less good at predicting forwards.
If you like the created model and want to run it again in future it would be wise to save it as a file (I’m not going to do that here though).
Using our Model for Prediction
I don’t have an unused data set to try the model on but I will apply it here back to the original dataset and see what we get.
#Use model to predict on full dataset
model_result = fpl_model.predict(X)
#Compute and print metrics
print('Accuracy: {}'.format(fpl_model.score(X, y)))
print(classification_report(y, model_result))
#Compute confusion matrix on whole data set
cnf_matrix = confusion_matrix(y, model_result)
#Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names,
title='Confusion matrix, without normalization')
#Plot normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
title='Normalized confusion matrix')
plt.show()
Accuracy: 0.8276643990929705
precision recall f1-score support
0 0.79 0.87 0.83 159
1 0.86 0.74 0.80 66
2 1.00 0.94 0.97 34
3 0.83 0.80 0.81 182
avg / total 0.83 0.83 0.83 441
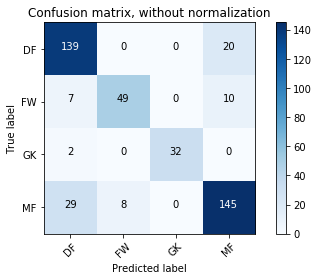
Confusion matrix, without normalization
[[139 0 0 20]
[ 7 49 0 10]
[ 2 0 32 0]
[ 29 8 0 145]]
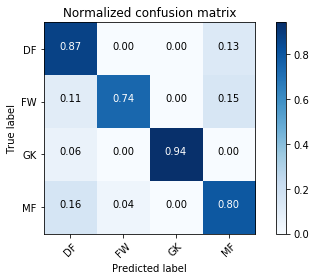
Normalized confusion matrix
[[ 0.87421384 0. 0. 0.12578616]
[ 0.10606061 0.74242424 0. 0.15151515]
[ 0.05882353 0. 0.94117647 0. ]
[ 0.15934066 0.04395604 0. 0.7967033 ]]
Thoughts
What, if anything, can we ascertain from these results? We can see from the confusion matrix on the full dataset that 8 midfielders were misclassified by our model as forwards. For fantasy players these misclassifications could provide a potentially interesting insight, as midfielders who act like forwards are likely to be valuable in fantasy terms. Lets see who these 8 players actually are.
To begin I’ll add the predictions back into the original dataset by adding a ‘Results’ column.
#Add model result to full dataset
fpl_data['Results'] = model_result
print(fpl_data.info())
<class 'pandas.core.frame.DataFrame'>
Index: 441 entries, Eldin Jakupovic to Asmir Begovic
Data columns (total 18 columns):
Position 441 non-null int64
Goals Scored 441 non-null int64
Assists 441 non-null int64
Clean Sheets 441 non-null int64
Goals Conceded 441 non-null int64
Own Goals 441 non-null int64
Penalties Saved 441 non-null int64
Penalties Missed 441 non-null int64
Yellow Cards 441 non-null int64
Red Cards 441 non-null int64
Saves 441 non-null int64
Bonus Points 441 non-null int64
Bonus Point System Score 441 non-null int64
Influence 441 non-null float64
Creativity 441 non-null float64
Threat 441 non-null int64
ICT Index 441 non-null float64
Results 441 non-null int64
dtypes: float64(3), int64(15)
memory usage: 85.5+ KB
None
Our new position column has been added and looks good. I’ll now do some DataFrame slicing and (just for clarity here) create a new DataFrame (fpl_wrong) that contains all the players our model misclassified. From that new DataFrame I’ll select the midfielders (class 3) who the model predicted as forwards (class 1).
#Create a new DataFrame of players who have been misclassified by the model
fpl_wrong = fpl_data.loc[fpl_data['Position'] != fpl_data['Results']]
#Select midfielders classified by our model as forwards
print(fpl_wrong[(fpl_wrong['Position'] == 3) & (fpl_wrong['Results'] == 1)])
Position Goals Scored Assists Clean Sheets \
Full Name
Gnegneri Yaya Toure 3 0 2 0
Adam Lallana 3 0 0 1
Junior Stanislas 3 5 3 2
Eric Maxim Choupo Moting 3 5 5 5
James McArthur 3 5 2 7
Wilfried Zaha 3 9 7 10
Richarlison de Andrade 3 5 8 8
Mohamed Salah 3 32 12 15
Goals Conceded Own Goals Penalties Saved \
Full Name
Gnegneri Yaya Toure 2 0 0
Adam Lallana 1 0 0
Junior Stanislas 22 0 0
Eric Maxim Choupo Moting 45 0 0
James McArthur 35 0 0
Wilfried Zaha 31 0 0
Richarlison de Andrade 54 0 0
Mohamed Salah 29 0 0
Penalties Missed Yellow Cards Red Cards Saves \
Full Name
Gnegneri Yaya Toure 0 1 0 0
Adam Lallana 0 1 0 0
Junior Stanislas 0 1 0 0
Eric Maxim Choupo Moting 0 3 0 0
James McArthur 0 5 0 0
Wilfried Zaha 0 5 0 0
Richarlison de Andrade 0 4 0 0
Mohamed Salah 1 1 0 0
Bonus Points Bonus Point System Score Influence \
Full Name
Gnegneri Yaya Toure 0 99 105.0
Adam Lallana 0 37 32.6
Junior Stanislas 7 285 394.8
Eric Maxim Choupo Moting 9 341 505.6
James McArthur 9 416 490.6
Wilfried Zaha 8 404 668.0
Richarlison de Andrade 4 304 497.0
Mohamed Salah 26 881 1496.2
Creativity Threat ICT Index Results
Full Name
Gnegneri Yaya Toure 122.6 72 29.8 1
Adam Lallana 113.4 128 27.3 1
Junior Stanislas 377.2 483 125.1 1
Eric Maxim Choupo Moting 327.5 851 168.1 1
James McArthur 333.0 566 138.9 1
Wilfried Zaha 716.9 1125 251.0 1
Richarlison de Andrade 384.7 1217 209.3 1
Mohamed Salah 942.5 2109 454.4 1
We have our 8 players. They include Mo Salah, the Premier League top scorer in the 2017/18 season. This is promising, if any player should be misclassified its Salah, a midfielder who scores 30+ goals a season. Another player is Zaha, in this current (18/19) seasons fantasy game he is no longer listed as a midfielder but as a forward, so this misclassification is also perfectly understandable. There is definitely scope here for checking this list between seasons to try and find potential value players for the following years game.
We’ll thats our k-NN Classification model! Its not perfect, we knew given the data limitations described in the intro it couldn’t be, but it still worked pretty well and could even be used to provide some insight into the fantasy Premier League game.

Leave a Comment